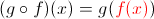Inverse Functions

1.5 Inverse functions

Finding inverse functions informally
ex. 
Find the inverse of f(x) = x - 6.  Then verify that both are equal to the identity function

You can verify that both functions are equal to the identity because: 

 
 


Definition of the inverse of a function

let f and g be two functions such that
       for every x in the domain of g
and
      for every x in the domain of f
We can conclude from this that, the function g is the inverse of the function f
Verifying inverse functions algebraically

ex.  Show that the functions are inverse of each other
     and       


                                             
                                           
                                           



                                         
                                         
                                         
Testing for one-to-one functions
ex. is one to one


   
   
      
Therefore,

implies that

So, f is indeed a one-to-one functions


Finding the inverse of a function

-Alec

One to One Functions

About One to One Functions:

One to one functions are defined as a relation of x,y where for every x there is only one value of y.

These functions have to pass the horizontal line test, because if there are multiple x values for the same y value, then the relation is not one to one.

The horizontal line test means that if you put a pencil horizontally on the graph of a given relation, and moves it up and down the y-axis, there would be only one point touching the pencil at a time.

Definition of One-to-One :

f(a)=f(b), a=b

Example 1:
This is an example of a one to one function. We can find out using the definition of a one to one function!

 f (x) = 3x - 4 

This is a one to one function because it passes the horizontal line test since it is linear, and makes the above equation true. 

    f(a)=f(b)

    3(a)-4=3(b)-4

    3a-4=3b-4

+4         +4

     3a=3b

     a=b

It's a... One to One Function!!

Example 2:
Take a look at the graph of this parabola. Shown here is the function f(x)=x^2 

Now, looking at this graph, we can decide it is not a one to one funciton because f(x)=x^2 does not pass the horizontal line test :(



Good to Know!

If a relation is a one-to-one function, it cannot be an even function

The inverse of a one-to-one function is also a function

Section 1.4

Another way of combining two functions is to form the composition of one with the other. 

Definition

The composition of the function     with     is 

Things to Remember!!!

and

IS NOT THE SAME AS 

Example 1

For instance, if:

and  

Remember:

So, the composition of       and  is

Example 2

For instance, if:

and    

  

                    

                                        

                   
Another version of this problem:                                                                   

       

Example 3

A case in which  

This means the functions are inverses of each other. For instance, if:

 and 

a 

                    

                    

                    

                    

               

                    

                    

                    

Extra Helpful Links!

Function Composition Video