The book's definition of an inverse trigonometric function is:
y = arcTRIG x if and only if TRIG y = x
With the domain and range being restricted
Evaluating
And because it is within the domain we can use the Unit Circle to help solve.
Negative pi over six is or answer because the sine of pi over six is equal to 1/2 therfore the inverse sine of 1/2 is equal to pi over 6.
Graphing
These are the normal sine, cosine, and tangent
sin y = x
cos y = x
tan y = xNow look at the inverse graphs of both and you can see what the difference is.
y = arcsin x
Note :
- That the graph is reflected in the line y = x
- It sill passes through (0,0)
- The Domain and Range have changed
y = arccos x
Note:
- This graph is also reflected in the line y = x
- It still starts at 1 just on the x axis instead of the y
- The Domain and Range have also changed
y = arctan x
Note:
- It is reflected in the line y = x
- It has horizontal asymptotes at pi over 2
- It's domain is now all real numbers
If you have an equation like:
What you can do is basically cancel out the tangent and inverse tangent so that your answer is just.
However when you don't have the same Trionometric function in the parenthesis. For instance:
Then you make the trig function in the parenthesis (in this case arcsin 7/4) and you set that equal to theta and make a right trianlge.
And you end up with the square root of 33 as your answer.
You then finish by solving using tangent.
And There Is Your Answer !!!











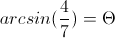





No comments:
Post a Comment