4.1 Radian and Degree Measure
Vocabulary:
Angle: determined by rotating a ray about its endpointInitial Side: starting position of a ray
Terminal Side: position after rotation of ray
Vertex: endpoint of a ray
Standard Position: angle in a coordinate system in which the origin is the vertex and the initial side coincides with the positive x-axis
Positive Angles: counterclockwise rotation
Negative Angles: clockwise rotation
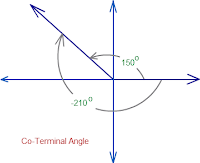
Co-terminal: angles that have the same initial and terminal sides
Radian: one radian is the measure of a central angle θ that intercepts an arc s equal in length to the radius r of a circle
Complementary Angles: 2 angles that sum is
 (90 degrees)
(90 degrees)Supplementary Angles: 2 angles that sum is π (180 degrees)
 about the vertex
about the vertexFormulas:
1. To convert degrees to radians, multiply degrees by2. To convert radians to degrees, multiply radians by
3. To find arc length, use the formula s=rθ, where s is arc length and r is radius of a circle
Examples:
Finding co-terminal angles:For the positive angle
 , subtract 2π to obtain a co-terminal angle.
, subtract 2π to obtain a co-terminal angle. Complementary and supplementary angles:
The complement of
 is
is The supplement of
is
Conversion between degrees and radians:
Convert 270° to radians:
Convert π/6 radians to degrees:
4.2 The Unit Circle
Vocabulary:
Periodic: Functions that behave in a cyclic manner where there exists a positive real number c such that f (t + c) = f (t)Period: The smallest number c for which f is periodic
Unit Circle:
Formulas:
Let r be a real number and let (x,y) be a point on the unit circle corresponding to r.The cosine and secant functions are even.
cos(-t) = cos t
sec(-t) = sec t
The sine, cosecant, tangent, and cotangent functions are odd.
sin(-t) = -sin t
csc(-t) = -csc t
tan(-t) = -tan t
cot(-t) = -cot t
Examples:
Evaluating Trigonometric Functions:Evaluate the sin of

Look at where the function corresponds to the unit circle.
Using the Period to Evaluate the Sine and Cosine:
Because

, you have
4.3 Right Triangle Trigonometry
Vocabulary:
Hypotenuse: the longest side of a right triangle, opposite the right angleOpposite Side: the side opposite the angle θ
Adjacent Side: the side adjacent to the angle θ
Angle of Elevation: the angle from the horizontal upward to the object
Angle of Depression: the angle from the horizontal downward to the object
Formulas:
Examples:
Applying Trigonometric Identities:Find the value of cos θ using the Pythagorean identity sin2θ + cos2θ = 1.
4.4 Trigonometric Functions of Any Angle
Vocabulary:
Reference Angle: the acute angle θ' formed by the terminal side of θ and the horizontal axisFormulas:
Examples:
Evaluating Trigonometric Functions:Given

θ lies in quadrant IV because it is the only quadrant in which the tangent is negative and the cosine is positive. Additionally,
Since y is negative in quadrant IV, let y = -5 and x = 4. So,
, and you have
4.5 Graphs of Sine and Cosine Functions
Vocabulary:
Sine Curve: graph of the sine function
Cosine Curve: graph of cosine function
Once Cycle: one period of the sine curve
Amplitude: half the distance between the maximum and minimum values ( y = a sin x and y = a cos x)
Period:
( y = a sin bx and y = a cos bx)
Formulas:
amplitude = | a |period: 2π/b
The period of sine and cosine curves is 2π.
C creates horizontal shifts of the sine and cosine curves
y = a sin (bx-c) and y = a cos (bx-c)
D creates vertical shifts of the sine and cosine curves
y = d + a sin(bx-c) and y = d+ a cos(bx-c)
4.6 Graphs of Other Trigonometric Functions
Vocabulary:
Tangent Curve: graph of the tangent functionCotangent Curve: graph of the cotangent function
Co-secant Curve: graph of co-secant function
Secant Curve: graph of secant function

Formulas:
The period of tangent and cotangent curves is π.The period of secant and co-secant curves is 2π.
4.7 Inverse Trigonometric Functions
Vocabulary:
Inverse Sine Function: arcsin x if and only if sin y = xInverse Cosine Function: arccos x if and only if cos y = x
Inverse Tangent Function: arctan x if and only if tan y = x
Examples:
Evaluating Inverse Trigonometric Functions:Find the value of arctan (-1).
Because
 and
and  lies in
lies in 
, it follows that
Using Inverse Properties:
Find the exact value of tan[arctan(-5)].
Because -5 leis in the domain of arctan x, the inverse property applies, and you have tan[arctant(-5)] = -5.

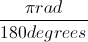





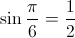

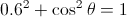





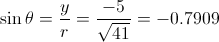






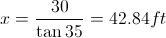
No comments:
Post a Comment