4.1 Trigonometry: Radian and Degree Measure

What is a radian?
The amount of rotation required such that the length of the intercepted arc is equal to the radius.

Angles 

• Angle-  Two rays with a common endpoint.  Angles are determined by rotating a ray about it's endpoint. 
• Initial Side- The starting position of the ray when measuring an angle
• Terminal Side- The position after the roation of a ray
• An angle can be positive or negative 
• How do we tell if it's positive or negative?  Angles are in standard position, where the vertex is at the origin, and the initial side is at the x-axis

              - Positive angles are generated by counterclockwise rotation
              - Negative angles by clockwise rotation.

• Can be measured in degrees or radians 

Angle Relationships

• Congruent- Angles with equal measures
• Complementary- Angles with measures that add up to 90

  °

   (or π/2 radians)
• Supplementary- Angles with measures that add up to 180

  °

   (or π radians)
• Coterminal- Two angles that when put in stardard position have terminal sides at the same spot

Coterminal angles 

Arc Length 

A circle has a radius of 4 inches.  Find the length of the arc intercepted by a central angle of 240°.

First, convert 240° to radians

240° = 240° ( π radians/180°)

4 π/ 3 radians

s=rθ

= 4(4π/3)

=16π/3 

= about 16.76 inches

Converting degrees to radians 

to convert degrees to radians, multiply degrees by π radians/180°( to cancel out the degrees)

135° =135 * (π radians/180°)= 3π/4 radians 

Converting radians to degrees

to convert radians to degrees, multiply degrees by 180°/π radians (to cancal out the radians) 

2 radians = 2 radians * (180°/ π radians ) = 114.59°

Complex Numbers

Imaginary Numbers

OK kiddies let’s learn section 2.4

Previously we have learned that there are only ‘real numbers’. Which makes sense how can there be numbers that are non-real or imaginary? Well in fact there are both real and imaginary numbers.

How can this be … Well how does one explain x= sqrt{-1} ?

No number we have learned can be inputted for x to solve this problem. So how can we square a number and get a negative result?

But if we "imagine" that we can … and it turns out that such a number, which may seem impossible, is actually useful and can solve real problems.

So… this is where imaginary numbers come in.

Imaginary numbers are: A number that when squared gives a negative result.

The "unit" imaginary numbers (the same as "1" for Real Numbers) is \[\sqrt{-1}\]  (the square root of negative one), and its symbol is i.

To solve follow this formula:

\[\sqrt{-a}\]= \[\sqrt{-1*a}\]= \[\sqrt{-1}\] * \[\sqrt{a}\]= a+bi where a is real and bi is imaginary

Example:

\[\Sqrt{-9}\] = \[\sqrt{9}\] * \[\sqrt {-1}\] = 3 and I written in a = bi form is 3i.

or

\[\Sqrt{-100}\] = \[\sqrt{100}\] *\[\sqrt{-1}\] = 10i.

So to review this is a breakdown of all numbers we have learned up to now…

Real numbers;

Rational or Irrational

Terminating decimals or Repeating decimals

Integers or Non integers

Whole numbers or Negative numbers

Natural numbers or zero

But this leaves us with one more dilemma what is a number that is compose of both a real and imaginary number such as

\[\Sqrt{-75}\] = 5i \[\sqrt{3}\]

Which is it real or imaginary?

Well it is both we call these numbers Complex numbers, they are a larger overarching group that includes all numbers.

So now the classifications look like:

Complex Numbers

Real numbers or imaginary

Rational or Irrational

Terminating decimals or Repeating decimals

Integers or Non integers

Whole numbers or Negative numbers

Natural numbers or zero

How to simplify complex numbers:

1)      i¹ = i

2)      i² = sqrt{-1} = -1

3)      i³ = i² * i¹ = -i

4)      i⁴= i² * i² = 1

This pattern of i, -1, -i, 1 repeats in this order for all degrees, so

what is i²²³ = ???

To solve divide 223/4 = 55 r.3
which means you can go through that repeating pattern 55 times and will stop on the third on or -i

So i²²³ = -i

 Post By: Tommy Scheidt

2.5 - Fundamental Theorem of Algebra and Complex Conjugate Pairs

Section 2.5 addresses the fundamental theorem of algebra as well as complex conjugate pairs.

Fundamental Theorem of Algebra

As quoted from the book, the theorem states...

"If f(x) is a polynomial of degree n, where n > 0, f has at least one zero in the complex number system."

The theorem also states that given an nth degree polynomial, the polynomial has n amount of roots, or zeros.

Example

Given the equation:

The polynomial is to the 1st degree, so we can conclude that there is one root, or zero. We can solve and confirm.

We solve and figure out that the equation has exactly one root: x = 2.

Yet we must remember that not all zeros are x-intercepts. Some zeros are found out to be imaginary.

Example 2

Given the equation:

We see that the polynomial is of the fourth degree. We can then conclude that it has four zeros. Let's solve and confirm.

Which is then split into two parts:

We can see that there are four zeros. Yet not all of them can be graphed. Two of them are imaginary. But, remember, they are still zeros!

Complex Conjugate Pairs

As seen in the previous section, roots of functions can be real, or imaginary. And as we also saw, the number of roots depends on the degree of the function. We will now learn that when an equation contains an imaginary root of form:

It will also contain the root:

From this we can conclude that there can only be an even number of imaginary roots. 

Also, be sure to remember that when eliminating imaginary numbers from denominators, multiply them by their conjugate, using the above form.

Long Division, Synthetic Division, Remainder Theorem, and Rational Root (Zero) Theorem

Ok kiddies, let's learn Section 2.3.

This post is terribly long due to all the steps needed to complete example problems.  Don't be afraid.

Long Division of Polynomials

Say I want to divide   by

First, I have to set up the problem itself.   is the divisor and  is the dividend.

It's not that scary...well actually...I guess it is a little bit scary.

Now that you've set up the problem, completely ignore most of the problem.  Focus only on the leading divisor and the leading dividend.

Your mission now is to figure out how many times x goes into ...     (  x * ? = )

...

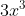
The answer is  in case you were wondering.

 

Long Division of Polynomials is very similar to Long Division that you learned when you were in Elementary school.  Your answer for the leading dividend goes above the second leading dividend, the answer for the second leading dividend goes above the third leading dividend, and so on.

Let's think about that 2.  Now that x has been multiplied by 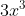, the same needs to happen to the 2 from .  Use the distributive property.

Remember this: When subtracting this from the dividend, PUT IT IN PARENTHESES FIRST! Otherwise, things will get very, very confusing.

Now you can distribute and continue on with the problem.

The leading values will cancel out, and now you just repeat this basic process to solve the rest of the problem. 

(x multiplied by what equals 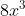, multiply the 2 by that answer, put it in parentheses, distribute, subtract, blah, blah, blah)

When you get to the very end and the last number does not equal zero, that is the remainder.  When writing the remainder, remember that the remainder is the numerator and the divisor is the denominator.

The correct way to write the final answer is 

BUT HOLD YOUR HORSES BATMAN! WHAT IF YOU HAVE A PROBLEM LIKE THIS?!

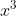
MISSING THE  VALUE? BLASPHEMOUS! 

Calm down champ.  Just do this.

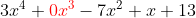
Synthetic Division

This method is much, MUCH faster than Long Division.  Long Division is called Long Division for a reason.

We'll use the same problem as last time:

 divided by 

To set up a problem and use Synthetic Division, simply take the coefficients from the polynomial and lay them out like so.

See where I took these numbers from?  They're simply the coefficients from largest to smallest value.

Now before you try a billion numbers on the left side of the box, read the problem again.

divided by 

 

Don't even think about plugging any number in besides the one given to you!

This is the pattern to solve this problem.

Any numbers in the vertical pattern are added together.

Any numbers in the diagonal pattern are multiplied by the number outside.

See? 3 is simply dropped down (or it is the result of 3+0) and then it is multiplied by 2 to equal 6 in the next column.  6 will then be added by 2...

...and the pattern continues and continues.

Now that the problem has been solved, it needs to be written out correctly.

The rightmost bottom number is the remainder. 

(The remainder is written the same way as it is in Long Division)

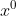
All powers of x reduce by one because the remainder takes the place of  coefficient.

Much faster and simpler than Long Division, yes?

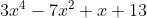
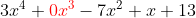
If     happens again, just remember to put a place holder for the missing x value, making the polynomial.  It is very important to list all coefficients when setting up the problem, even if some of them are zero.

Remainder Theorem

If a polynomial f(x) is divided by x-k, the remainder is r=f(k)

This sounds confusing and it is.

We'll use our beloved problem again.

  divided by 

What this is saying that if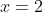 

 and the remainder is 51,

 then 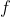(2)=51,

 and (2, 51) is a point on the graph of .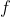

 This can be confirmed by substituting x=2 in the original function.

=51

Rational Root Theorem

Possible rational zeros          =           factors of constant term

                                                        factors of leading coefficient

Couldn't use the example I've used

throughout the entire post

because it doesn't have

any zeros :'(

The leading coefficient is 2 and the constant term is 3.

    factors of 3             =              

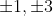
        factors of 2                               

= 

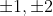
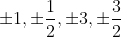
(1/1=1, 1/2=1/2, 3/1=3, 3/2=3/2)

From here, use synthetic division to test these eight possibilities.

Conveniently, positive 1 works.

That means that x=1 is a zero.

If you plug a zero you've found back into original function, you can find the other zeros without using Synthetic Division!

                                              

                                                       

                                                                           

Tada!

You made it to the end of the post.

Congratulations.