Finding the Sum of Two Functions
Equation for the Sum:
To find the Sum of two functions, just like real numbers, simply add the two functions together.
Example:
Find
for the functions
and 
. Then evaluate the sum when 
.
Finding the Difference of Two Functions
Equation for the Difference:
To find the Difference of two equations, just like real numbers, simply subtract the equations. (Make sure to pay attention to the order in which the equations are to be subtracted).
Evaluate
for the functions 
and 
when .
for the functions and when .
Finding the Product of Two Functions
Equation for the Product:
To find the Product of two equations, just like real numbers, simply multiply the equations. (Pay careful attention to exponents).
Given the functions
and 
, find the product of 
and 
. Then evaluate the product when 
.
and , find the product of and . Then evaluate the product when .
Find the Quotient of Two Functions
Equation for the Quotient:
,
,
To find the Quotient of two equations, just like real numbers, divide the equations. (Make sure to pay attention to the order in which the equations are to be divided).
ATTENTION: If asked to find the domain of the new equation, which is very likely, one must check for solutions that don't work. This is required because of the rule that the denominator cannot equal zero.
Find
and 
for the functions 
and 
. Then find the domains of 
and 
.
and for the functions and . Then find the domains of and .
The quotient of and is:
and is:
The quotient of
and is:
The domain of is 
{see original equation}
is {see original equation}
The domain of is 
{see original equation}
is {see original equation}
The domain of
is 
is
The reason that there is a bracket around the "0" is because
can equal zero without the answer being undefined and "0" is the lowest number in our set of inputs
can equal zero without the answer being undefined and "0" is the lowest number in our set of inputs
The reason that there is a parenthesis around the "2" is because must be less than "2" otherwise the answer will be undefined
must be less than "2" otherwise the answer will be undefined
The domain of
is 
is
The reason that there is a parenthesis around the "0" is because if equalled "0", the answer would be undefined because the square-root of zero is zero
equalled "0", the answer would be undefined because the square-root of zero is zero
The reason that there is a bracket around the "2" is because can be less than or equal to "2"
can be less than or equal to "2"
It must stop at "2" because that is the highest number of the domains in the previous sections:
The domain of is {see original equation}
is {see original equation}
The domain of is {see original equation}
is {see original equation}
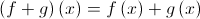
No comments:
Post a Comment