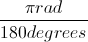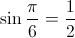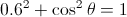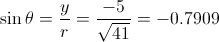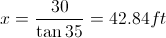4.1 Radian and Degree Measure
Vocabulary:
Angle: determined by rotating a ray about its endpointInitial Side: starting position of a ray
Terminal Side: position after rotation of ray
Vertex: endpoint of a ray
Standard Position: angle in a coordinate system in which the origin is the vertex and the initial side coincides with the positive x-axis
Positive Angles: counterclockwise rotation
Negative Angles: clockwise rotation
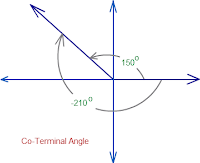
Co-terminal: angles that have the same initial and terminal sides
Radian: one radian is the measure of a central angle θ that intercepts an arc s equal in length to the radius r of a circle
Complementary Angles: 2 angles that sum is
(90 degrees)Supplementary Angles: 2 angles that sum is π (180 degrees)
about the vertex
Formulas:
1. To convert degrees to radians, multiply degrees by
2. To convert radians to degrees, multiply radians by
3. To find arc length, use the formula s=rθ, where s is arc length and r is radius of a circle
Examples:
Finding co-terminal angles:For the positive angle
, subtract 2π to obtain a co-terminal angle. 
Complementary and supplementary angles:
The complement of
is 
The supplement of
Conversion between degrees and radians:
Convert 270° to radians:
Convert π/6 radians to degrees:
4.2 The Unit Circle
Vocabulary:
Periodic: Functions that behave in a cyclic manner where there exists a positive real number c such that f (t + c) = f (t)Period: The smallest number c for which f is periodic
Unit Circle:
Formulas:
Let r be a real number and let (x,y) be a point on the unit circle corresponding to r.
The cosine and secant functions are even.
cos(-t) = cos t
sec(-t) = sec t
The sine, cosecant, tangent, and cotangent functions are odd.
sin(-t) = -sin t
csc(-t) = -csc t
tan(-t) = -tan t
cot(-t) = -cot t
Examples:
Evaluating Trigonometric Functions:Evaluate the sin of
Look at where the function corresponds to the unit circle.
Using the Period to Evaluate the Sine and Cosine:
Because
, you have
4.3 Right Triangle Trigonometry
Vocabulary:
Hypotenuse: the longest side of a right triangle, opposite the right angleOpposite Side: the side opposite the angle θ
Adjacent Side: the side adjacent to the angle θ
Angle of Elevation: the angle from the horizontal upward to the object
Angle of Depression: the angle from the horizontal downward to the object
Formulas:
Examples:
Applying Trigonometric Identities:Find the value of cos θ using the Pythagorean identity sin2θ + cos2θ = 1.
4.4 Trigonometric Functions of Any Angle
Vocabulary:
Reference Angle: the acute angle θ' formed by the terminal side of θ and the horizontal axisFormulas:
Examples:
Evaluating Trigonometric Functions:Given
θ lies in quadrant IV because it is the only quadrant in which the tangent is negative and the cosine is positive. Additionally,
Since y is negative in quadrant IV, let y = -5 and x = 4. So,
4.5 Graphs of Sine and Cosine Functions
Vocabulary:
Sine Curve: graph of the sine function
Cosine Curve: graph of cosine function
Once Cycle: one period of the sine curve
Amplitude: half the distance between the maximum and minimum values ( y = a sin x and y = a cos x)
Period:
( y = a sin bx and y = a cos bx)
Formulas:
amplitude = | a |period: 2π/b
The period of sine and cosine curves is 2π.
C creates horizontal shifts of the sine and cosine curves
y = a sin (bx-c) and y = a cos (bx-c)
D creates vertical shifts of the sine and cosine curves
y = d + a sin(bx-c) and y = d+ a cos(bx-c)
4.6 Graphs of Other Trigonometric Functions
Vocabulary:
Tangent Curve: graph of the tangent functionCotangent Curve: graph of the cotangent function
Co-secant Curve: graph of co-secant function
Secant Curve: graph of secant function
Formulas:
The period of tangent and cotangent curves is π.The period of secant and co-secant curves is 2π.
4.7 Inverse Trigonometric Functions
Vocabulary:
Inverse Sine Function: arcsin x if and only if sin y = xInverse Cosine Function: arccos x if and only if cos y = x
Inverse Tangent Function: arctan x if and only if tan y = x
Examples:
Evaluating Inverse Trigonometric Functions:Find the value of arctan (-1).
Because
and 
lies in 
, it follows that
Using Inverse Properties:
Find the exact value of tan[arctan(-5)].
Because -5 leis in the domain of arctan x, the inverse property applies, and you have tan[arctant(-5)] = -5.
4.8 Applications and Models
Formulas:
Examples:
While searching for Christmas trees, Jimmy spots the perfect tree in the distance. The angle of elevation to the top of the tree is 35 degrees. How many more feet must Jimmy walk to get to the tree?
