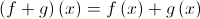Finding the Sum of Two Functions
Equation for the Sum:
To find the Sum of two functions, just like real numbers, simply add the two functions together.
Example:
Find
 for the functions
for the functions and
and  . Then evaluate the sum when
. Then evaluate the sum when  .
.
Finding the Difference of Two Functions
Equation for the Difference:
To find the Difference of two equations, just like real numbers, simply subtract the equations. (Make sure to pay attention to the order in which the equations are to be subtracted).


Finding the Product of Two Functions
Equation for the Product:
To find the Product of two equations, just like real numbers, simply multiply the equations. (Pay careful attention to exponents).



Find the Quotient of Two Functions
Equation for the Quotient:
To find the Quotient of two equations, just like real numbers, divide the equations. (Make sure to pay attention to the order in which the equations are to be divided).
ATTENTION: If asked to find the domain of the new equation, which is very likely, one must check for solutions that don't work. This is required because of the rule that the denominator cannot equal zero.

The quotient of
 and
and  is:
is:
The reason that there is a bracket around the "0" is because can equal zero without the answer being undefined and "0" is the lowest number in our set of inputs
can equal zero without the answer being undefined and "0" is the lowest number in our set of inputs
 can equal zero without the answer being undefined and "0" is the lowest number in our set of inputs
can equal zero without the answer being undefined and "0" is the lowest number in our set of inputs
The reason that there is a parenthesis around the "2" is because  must be less than "2" otherwise the answer will be undefined
must be less than "2" otherwise the answer will be undefined
 must be less than "2" otherwise the answer will be undefined
must be less than "2" otherwise the answer will be undefined
The reason that there is a parenthesis around the "0" is because if equalled "0", the answer would be undefined because the square-root of zero is zero
equalled "0", the answer would be undefined because the square-root of zero is zero
 equalled "0", the answer would be undefined because the square-root of zero is zero
equalled "0", the answer would be undefined because the square-root of zero is zero
It must stop at "2" because that is the highest number of the domains in the previous sections: